Saturday bring us another great science talk in the Palmer. This time Dr. Thomas Decloedt, from the University of Hawaii, explained the use of the ADCP and LADCP for measuring ocean currents.
Dr. Thomas Decloedt, a very friendly scientist aboard the Palmer, is in charge of the LADCP
When I have written about the ADCP in this journal I have said they measure the currents in the same way the police measures the speed of a car, but I did not explain how it is done. I will attempt to explain here the doppler effect. Again, there are lots of wonderful books that explain this better than I can do here, so I urge you to read them if you end up confused by my attempt.
Think about a time in which you were standing on a sidewalk or seating in your car while it was not moving, and an ambulance or fire truck passed by at great speed with its siren on. You probably heard the siren with a higher pitch when it was going towards you than how it sounded when it was moving away from you. That is due to the doppler effect.
The doppler effect happens when there is a source of pulses or waves that is moving with respect to an observer. In the case of the ambulance, the siren is the source of waves and you are the observer. It does not matter if the source moves or you move, in both cases one moves with respect to the other.
We need to define frequency in order to understand the doppler effect. Frequency is defined as the number of pulses or waves that pass by a certain place in a given time. We can talk about your heart's frequency as an example. You count the number of heart pulses in a minute and you get your heart's frequency. If you run for 15 minutes you will see that your heart's frequency increases (more pulses in a minute). Sound is a wave, and we hear the frequency as the pitch of the sound. High frequency means high pitch and vice-versa.
Now imagine you are standing in front of a small pond and that you throw a rock that does not skip to the center of the pond. Ripples will emanate from the place in which the rock landed. The ripples are waves that travel in expanding circles that have a common center, where the rock hit the water. We call 'concentric circles' to circles that have a common center. You can find the frequency of the ripples by counting the number of ripples that arrive to the shore of the pond in a minute. If you were to count the number of ripples that arrive to the shore on the other side of the pond you will find that the frequency is the same as in your side.
Now imagine there is one of those insects that walk on the water surface making the ripples. If the insect does not advance, but still moves its legs, it generates ripples just like the rock did, and you can find its frequency by counting the number of waves that arrive at one point in a minute. This frequency would, again, be the same on both ends of the pond.
The insect is very curious and decides to check you out, so it begins to move towards you and generates the same ripples. The key here is that the second ripple is generated in a spot that is closer to you than where the first ripple was generated. The third ripple is generated even closer to you and so on. The ripples are no longer concentric circles; each circle is embedded on another circle as long as the insect is slower than the waves it generates, but closer to one side of the larger circle than to the other side.
A bug walking in water shows how the circular ripples generated when it does not move are concentric but stop being concentric as soon as it begins moving. The frequency on the right of the bug, the direction in which the bug is moving, is higher than on the left.
Notice that the distance between two circles is shorter on the side towards the insect is moving than the distance between circles on the back. We will assume that all the ripples travel at the same speed. If we count the number of ripples that get to the shore where you are you will find that there are more ripples per minute (higher frequency) than the ones arriving on the shore on the other side of the pond (lower frequency) in the same amount of time. This means the ripples have a higher frequency on your side of the pond than on the other side, even when the insect generates the ripples at a constant frequency.
All this to say that when a wave source is in motion relative to an observer, the frequency at which the observer perceives the waves is different from the frequency at which waves are generated. When the source is moving towards the observer, the frequency increases, and when it moves away from the observer, the frequency decreases. If we look back at the ambulance example, you hear a higher pitch of the siren when it moves towards you because the sound frequency increases, and you hear a lower frequency when it moves away because the frequency decreases.
The person to the right of the picture, towards where the ambulance is moving, hears a higher pitch siren than the one on the left due to the doppler effect.
The police can figure your velocity by sending an ultrasound wave at a known frequency towards your car. The waves reflect from your car and the frequency changes depending on your speed. If your car is stopped, the radar gun receives the ultrasound at the same frequency at which it was sent. If you are moving towards the officer, on the other hand, the gun receives the ultra sound at a higher frequency. The difference in frequency between the ultrasound sent by the radar gun and the one that bounced back from your car is proportional to your speed. The officer can use this information to find out your velocity. One limitation of the method is that this works only if the ultrasound beam is parallel to the direction in which the car travels. This means that the radar gun can only measure the speed at which the car is moving towards the gun or away from the gun; it cannot measure the speed of a car that is moving perpendicular to the direction of the gun. That is why police use this guns in parts of the roads that are long and straight.
The officer on the left of the car can find the car's velocity, but the one below cannot as the doppler effect only works when the waves are parallel to the direction of the motion between observer and wave source.
We finally get back to the ADCP, which stands for Acoustic Current Doppler Profiler (an instruments that measures currents by sending sound waves and measuring the doppler shift on frequency). The ADCP is the radar gun, and for it to work in needs cars to be moving. The cars are anything small floating in mid water that moves with the currents. The fancy name for this is 'scatterers'. Most of them are what Thomas called 'bugs' and biologists call plankton. Thomas said that they have found places in the oceans with so few plankton that the ADCP does not work well because there are not enough scatterers.
LADCP on top of the rosette. The two yellow circles are two of the LADCP transducers from where it sends and receives the acoustic signals. The other two transducers are not visible.
Remember that the radar gun cannot measure the speed of the car when it moves perpendicular to the ultrasound beam. This would mean the ADCP could only measure the speed back and forth in one direction. We solve this problem by placing four 'guns' on the ADCP, called transducers, pointing on four directions. We can then resolve the currents in any direction. The amazing thing about the system is that you can set the ADCP to measure the velocity of the bugs at different distances from the ADCP allowing us to obtain a profile (therefore the name of profiler). This means that we can measure the currents at different depths! Fantastic, don't you think?
The LADCP stands for Lowered ADCP. This is an ADCP that is attached to the rosette and measures the currents along the 4500 meters of depth that our rosette travels. That is even better than the ADCP that is attached to the boat. It is a bit more complicated to get the currents from the LADCP because the LADCP is also moving. We need to somehow remove the motion of the rosette so we can isolate the motion of the currents. It is better two have to LADCP on the rosette, one pointing to wards the surface and another towards the bottom. Thomas can use the data from both LADCP and the ADCP from the ship to get the velocity of the currents.
Thomas showed this image of the current averages between 100 m and 500 m of depth and another one of one of the sections we have done. His data generated more scientific questions that we hope will be able to resolve with the data from Alex's moored current meters that we recovered.
Vectors showing the velocity averages for the 100 m to 500 m depths. The arrows point in the direction towards where the currents flow and the length of the arrow gives the speed.
One really neat thing shown by Thomas is that he can also resolve the horizontal motions of the rosette during the cast He showed us this image from one of our casts. You can see where the rosette left the boat, the big circles that it made and where it ends back on board.
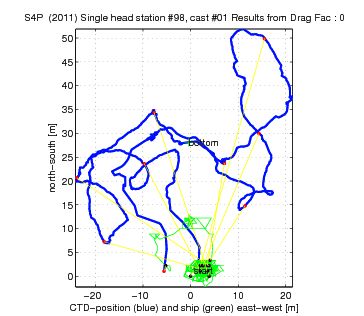Horizontal motion of the rosette during a cast. The starting point is on the right side and the ending point on the left.