Look at he following picture and What is wrong with the following picture and think about what is wrong. It shows the same laboratory scale with the same objects on top.
Same scale gives two correct weights for the same objects due to changes in acceleration
There is nothing wrong. The objects are going through what I call weight swings. How can this be?
Your weight depends on two things, your mass (how much stuff you are made of), and the acceleration with which you fall to the ground caused by the gravitational attraction with the earth. Acceleration is the change in an object's motion, either speeding up, slowing down or changing direction in which an object moves. In other words, your weight is a force, and Newton defined long time ago a force as the product of the mass and the acceleration of the object (F = m*a).
Your weight will change if you either change your mass, or change the acceleration due to gravity (called 'g'). So next time you want to loose weight, forget about the diets and travel to a very tall mountain; the gravitational acceleration depends on the earth's mass and the distance between you and the earth. The farther you move away from the center of the earth, the less gravity you will feel and the less you weight. It works for astronouts when they are in outer space.
You already know that you fall down when the only force acting on you is the gravitational force. You begin at a speed of 0 m/s (no motion), and your speed begins to increase (one form of acceleration). How much are you accelerating? Every second your speed increases by 9.8 m/s. You start at 0 m/s; after one second you move at 9.8 m/s, and after 2 seconds you move at 19.6 m/s and so on. This means that the value of g is 9.8 m/s every second, or g=9.8 m/s2 (s2 = s*s).
Acceleration, like velocity, is a vector quantity (defined on April 4). We can use a bold type for vectors to distinguish them from scalars: g is scalar and does not include direction, while g is a vector that includes direction. To fully describe acceleration we need to specify the amount (9.8 m/s2) and the direction in which it operates (g acts downwards. We use the minus sign to indicate this, therefore g = -9.8 m/s2). Vectors can be added just like numbers, so accelerations can also be added. We can think of forces acting on you as accelerations, since your mass does not change.
Let us go back to the objects on the scale in the pictures above. The objects do not change mass, but their weight does change. This means that the acceleration on them is changing. The pictures where taken on the ship on a day of large waves. This means that the ship was moving up an down with the waves in a mater of seconds, and so was the scale. Think about the objects on the scale. When the scale moves up, the objects tend to stay where they are (we call this inertia); they accelerate downwards with respect tot the scale. Since the gravitational acceleration points downwards, both accelerations add up to produce an even bigger acceleration also pointing downwards. The objects weight more with respect to the moving balance.
When the ship and scale move downwards, the objects accelerate upwards with respect to the scale. When we add this acceleration pointing up with the gravitational acceleration pointing down we end up with an acceleration that points down that is less than the gravitational acceleration, or even an acceleration that points up within the scale mechanism. When the acceleration points up, the scale gives a negative weight.
The scale then becomes useless for determining an object's weight, but useful for determining the acceleration if you know the object's weight ahead of time. We call this an accelerometer. The scale is a very crude accelerometer.
Next time you ride on an elevator bring you scale and see that you weight less when the elevator moves downwards and weight more when it moves up, just like we do on the ship. The difference is that it in the ship the acceleration is constantly changing.
There are devices that can measure the changes in acceleration that are smaller than the scale and objects that I used. In fact, if you own an Apple laptop you own one of such devices. Apple engineers installed an accelerometer on the laptops so when the computer falls the accelerometer registers the change in acceleration and makes the hard drive stop spinning so it does not get harmed. They might stop installing the accelerometer now that we are shifting towards solid state memory.
Some people have written programs that can tap on the laptop's accelerometer. One such program is called SeisMac; designed to register earthquakes (seismic activity, therefore the name SeisMac). SeisMac produces a graph of the total acceleration felt by the computer, which is the gravitational acceleration plus the acceleration due to the motion of the ground. It separates the motion in two horizontal components (X and Y) and one vertical component (Z).
SeisMac also works for measuring the acceleration due to the motion of the ship by the waves! Chris Measures gave me a copy of the free program when he saw I was building my own crude accelerometer with the scale. My accelerometer only measures vertical acceleration, but SeisMac can also tell if the ship is accelerating to the sides.
The program needs to be calibrated when the ship is not moving, something I should have done when we were wedged on the ice during the ice party, but I forgot. Without any acceleration besides the gravitational acceleration, it should read 1.00 g, or one gravitational acceleration (g = -9.8 m/s2). Since mine is not calibrated, it will show oscillations somewhere around 1.07 g. I will know the exact value once we get to Punta Arenas. Here is the screen output on a day with barely any waves.
Acceleration felt by my computer on a day with small and long waves.
The vertical axis in the plot corresponds to the acceleration in multiples of g (1 g = -9.8 m/S2), and the horizontal axis is time. Vertical blue lines appear every 10 seconds, and the green horizontal line represents 1.00 g. You can see that the acceleration oscillates with long hills and valleys and very small wiggles on top of the hills. The small wiggles are the acceleration produced by the vibrations in the ship. The highest value in this graph is around 1.12 g and the lowest values are close to 1.03 g. Let us look at a day with a few more waves.
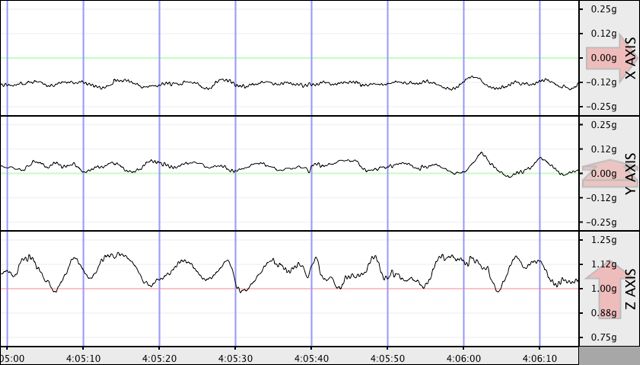Acceleration felt by my computer on a day with medium waves.
The hills are taller now, and closer together. Notice that most of the acceleration is vertical (Z), with a little bit on the horizontal (X and Y). The highest value is around 1.18 g this time, and the smallest is around 0.90 g. I am sure you would like to see the acceleration measured on a day with larger waves:
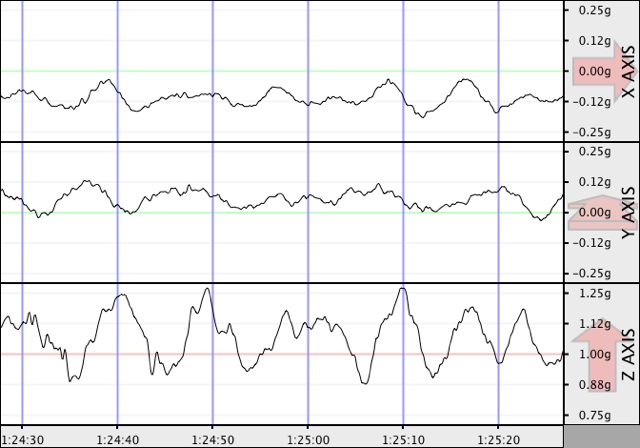Acceleration felt by my computer on a day with large waves.
You can also see that the ship this time was also moving more in the horizontal. The largest value in the vertical was above 1.25 g this day, and smallest around 0.88 g. Wow! This means that if I weight around 70 kg in McMurdo Station, at sea level, that day in the ship my weight was constantly changing, without considering the calibration error, between 87.5 kg and 61.6 kg in a matter of seconds. That is what I call having weight swings!
The ship swings are larger in the bridge because it is higher up in the ship (farther form the ship's center of mass). I have been waiting for a day with big waves to take the laptop to the bridge, but we have been enjoying very calm seas during the past two weeks (which is good for me, by the way). Even now that we are in the middle of the Drake Passage it does not seem as bad as in some storms we had before. Here is the graph for the Crossing of the Drake Passage as registered int he bridge. Notice the change in the vertical scale. The largest acceleration is about 1.30 g and the smallest 0.80 g (my weight would has been between 91 kg and 56 kg).
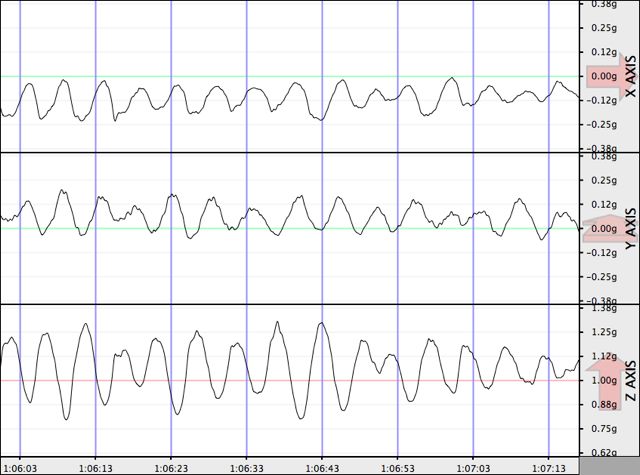Acceleration felt by my computer while crossing the Drake Passage.